up-sweep(掃き上げ)での更新は「Prefix-Sumの要素分解図」(表15.3「表:Prefix-Sumの要素分解図(括弧内の数は式番号に該当)」)と「図15.1「Bucket Scanの算出式(要素8の場合)」」のプロセスの内、出力配列の計算を抜いた部分となります。
up-sweepは以下の擬似コードで表すことができます。
擬似コード:掃き上げ.
for( d = 0 ; d < log(n) - 1 ; d++)
for( i = 0 ; i < n ; n+=2のd+1乗)
x[i + 2のd+1乗 – 1] =
x[i + 2のd乗 – 1] +
x[i + 2のd+1乗 – 1]
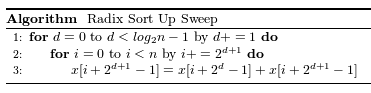
このコードでは、dはアルゴリズムのステップを指し、0から始めます。まずdが0の場合を見てみましょう。
d = 0 i = 0, 2, 4, 6 x[i + 1] = x[i] + x[i + 1]
dが0の場合に更新されるインデックスは(0,1)、(2,3)、(4,5)、(6,7)となります。単純に隣接した要素を偶数のインデックスの位置を起点に加算します。
d = 1 i = 0, 4 x[i + 3] = x[i + 1] + x[i + 3]
dが1の場合に更新されるインデックスは(1,3)、(5,7)となります。ステップで算出した値をさらに加算・累積していきます。
d = 2 i = 0 x[i + 7] = x[i + 3] + x[i + 7]
最後にdが2の場合ですが、更新されるインデックスは(3,7)となります。インデックス7の要素は、要素を全て加算した数値にアップデートされます。
下記の表はup-sweepアルゴリズムの各ステップをまとめたものです。
注目すべき点としては「更新された入力配列」がこの時点ではPrefix-Sumを構成しないことです。
以下の項目では、down-sweepを使いPrefix-Sumとなる配列を作ります。