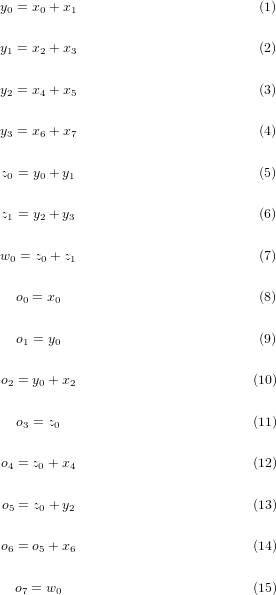BucketスキャンはPrefix-Sumを計算する段階を指します。Prefix Sumは下表のように算出することができます。

Prefix-Sumの計算は並列化に適しています。例としては、8つの要素を持つ入力配列のPrefix-Sumを求めてみましょう。

xを入力配列として、部分和をy,z,wとして、出力配列（Prefix-Sum）をoとします。

図15.1 Bucket Scanの算出式（要素8の場合）

計算式は回路図とすることもできますが、８要素の場合は以下の表のようにしてみるだけでも自明かと思います。

x0

x1

x2

x3

x4

x5

x6

x7

y0(1)

y1(2)

y2(3)

y3(4)

z0(5)

z1(6)

w0(7)

o0

o1

o2

o3

o4

o5

o6

o7

各要素の計算を並列化するとアルゴリズムのステップ数（段階）はわずか4つとなります。

これをシングルスレッド（workitem=1）の直列的な計算とすると以下のようなソースコードとなります。

for(int i = 1; i < size; i++)
    count[i] += count[i-1];

入力配列の要素がビッグデータ（数百億以上）となるような場合には、明らかなボトルネックとなります。

無論、弱点としてはシーケンシャルな計算量はO(n)となりますが、部分和を使うアルゴリズムの計算量はO(nlogn)となり、並列コアの大小によっては得られるパフォーマンス上の利点が消える可能性もあります。

対策としてはReduction法（又はReductionパターン）を使うことです。これは次の項目で解説します。