掃き下げは、掃き上げで更新した入力配列を再分解していき、さらにその部分和を各ステップでおこない、累積値を計算していきます。

掃き下げのリファレンスアルゴリズムは以下のコードで表すことができます。

擬似コード：掃き下げ. 

x[n-1] = 0
for( d = log(n)-1 ; d < 0 ; d--)
    for( k = 0 ; k < n ; k += 2の（d+1）乗)
            tmp = x[k + 2^{d}–1]
            x[k + 2^{d}–1] =
                x[k + 2^{d+1} – 1]
            x[k + 2^{d+1} – 1] =
                tmp + x[k + 2^{d+1} – 1]
    end
end

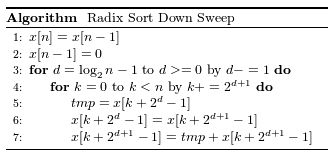
擬似コードの第一のforループにあるd=2の場合を考えて見ましょう。この場合ではkは、k=0のみとなり、１回だけループをします。

d = 2
k = 0
tmp = x[k + 3]
x[k + 3] = x[k + 7]
x[k + 7] = tmp + x[k + 7]

つまり添字3と7の間での処理をします。次にdが1の場合を見てみましょう。

d = 1
k = 0, 4
tmp = x[k + 1]
x[k + 1] = x[k + 3]
x[k + 3] = tmp + k[x + 3]

この事例では、kは0と4の数値をとるので、ループは2回反復をします。対象となる添字は、（1,3）、（5,7）の2セットです。

最後にdが0の場合を見てみましょう。

d = 0
k = 0, 2, 4, 6
tmp = x[k]
x[k] = x[k + 1]
x[k + 1] = tmp + x[k + 1]

対象となる添字は、(0,1)、(2,3)、(4,5)、(6,7)となります。これらの更新は以下の表にまとめられています。

x0

x1

x2

x3

x4

x5

x6

x7

元データ

1

5

10

7

4

15

2

9

入力

1

6

10

23

4

19

2

53

0

更新2 

 x3 -> x7, x7 -> x3

d=2

x7

x3

d=2

0

23

更新1 

 x1 -> x3, x3 -> x1, x7 -> x5, x5 + x7 -> x7

d=1

x3

x1

x7

x5+x7

d=1

0

6

23

42

更新0 

 x1 -> x0, x0 -> x1, x3 -> x2, x2 + x3 -> x3, x5 -> x4, x4 + x5 -> x5, x7 -> x6, x6 + x7 -> x7

d=0

x1

x0

x3

x2+x3

x5

x4+x5

x7

x6+x7

入力->出力

0

1

6

16

23

27

42

44

出力された数値が「元の入力値」の累積ヒストグラムとなっていることが確認できます。up-sweepで算出した総和53を加えてPrefix Sumは完成します。