目次
バイトニックソートは「Ken Batcher」が考案した並列ソートアルゴリズムです。完成度の高い並列化が可能なため、基数整列(radix sort)と同様にGPUでの整列アルゴリズムに適しています。
パフォーマンス上では、Radix Sortより劣りますが、一旦理解ができるようになると直感的に説明ができるようになることはアルゴリズムとしては大きな利点と言えるかと思います。
また並列コアを一定して使用させることができるため、最適化する余地が少ないことが、基数配列と比べて好まれる要因ともなっているようです。
バイトニック配列(またはシーケンス、シークエンス等)は以下の2つの式で表すことができます。
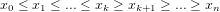
配列の要素はある一定の要素(配列の最大値)まで上昇し、そこから下降していきます。
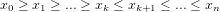
もしくは配列の要素はある一定の要素(配列の最小値)まで下降し、そこから上昇していきます。本書ではバイトニックを一義的に前者として定義します。
バイトニックソートは、このバイトニック配列を2つのバイトニック配列にする「バイトニック分割(Bitonic Split)」を行い、片方は少ない値、もう片方は大きい値をとる配列に分割し、分割した配列を上昇形態と下降形態に整列する「バイトニック結合(Bitonic Merge)」を繰り返します。
バイトニック分割を具体的に行なう場合は、バイトニック配列の添字(インデックス)を2つに分けます。そして2つに分けた配列の要素を以下の式で比較します。
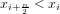
この式が成立した場合に、値をスワップ(入れ替え)します。これはバイトニック配列の上昇形態の部分の場合で、下降形態の部分配列では不等式は反対の方向性の関係を持ちます。
バイトニック結合は上昇形態と下降形態に分割された配列を結合(整列)します。結合は分割より一段低いnの値で上昇形態、下降形態に整列します。
バイトニック整列は複雑なので、一見理解できなくとも流れだけを見るとわかるようになるアルゴリズムです。まず具体的なアルゴリズムの手順をご覧いただきます。
バイトニック整列のアルゴリズムは、ステージ(Stage)というマクロレベルのステップ、ステージ内のサブステップとなるパス(Pass)からなります。
Stageが0の場合は、比較する要素の距離は1となり、ステージ1となると距離は2、ステージ2で距離が4、ステージ3で要素間の距離が8の比較を行います。データの要素数が増えるに従って処理すべきステージの総数は増加します。(原則として整列する配列は2の累乗のみ。0を挿入して2の累乗に補完するテクニックもあります。)
パス(Pass)は0の場合がやや特殊例となり、上昇・下降のバイトニック分割(Bitonic Split)に該当します。パスはステージが0の場合は0のみ、ステージが1の場合は0と1、ステージが2の場合は0と1と2というようにステージの回数に1を足した回数を繰り返します。
本書ではパスが0以外のステップをバイトニック結合(Bitonic Merge)として定義しますが、このバイトニック結合は、分割で決定された上昇形態となる配列インデックス(添字)、下降形態となる配列インデックス(添字)となるように整列をします。
分割と結合の具体的な過程は以下に具体例を出すのでそれで確認してください。
「表:Bitonic Split(Stage=0,Pass=0)」(表14.1「表:Bitonic Split(Stage=0,Pass=0)」)では、8つの配列要素を、各2つのバイトニック配列に分割しています。
データのインデックス(0,1,4,5)が上昇形態、(2,3,6,7)が下降形態とするバイトニック配列を作ります。
この例では以下のように不等式がなりたたない場合、各要素のスワップ(入れ替え)を行います。
- 【上昇形態】3 < 7(インデックス:0と1)
- 【下降形態】12 > 98(インデックス:2と3)、要素をスワップ
- 【上昇形態】78 < 66(インデックス:4と5)、要素をスワップ
- 【下降形態】6 > 5(インデックス:6と7)
左半分【3,7,98,12】、【12,66,6,5】の2つのバイトニック配列に分割されました。
次の分割ステップ、「表:Bitonic Split(Stage=1,Pass=0)」(表14.2「表:Bitonic Split(Stage=1,Pass=0)」)では、2つのバイトニック配列を1つにします。
このステップでは、インデックスの(0,1,2,3)が上昇形態、(4,5,6,7)が下降形態とするバイトニック配列を作ります。
上記の表では以下の不等式とスワップが行なわれます。
- 3 < 98(インデックス:0と2)
- 7 < 12(インデックス:1と3)
- 66 > 6(インデックス:4と6)
- 78 > 5(インデックス:5と7)
比較の結果、要素のスワップは行われません。
「Bitonic Split(Stage=1,Pass=0)」(表14.2「表:Bitonic Split(Stage=1,Pass=0)」)は分割したのみで、バイトニック整列の構成用件を満たしません。左半分が上昇形態、右半分が下降形態とするならば、【3,7,12,98】, 【78,66,6,5】とならなければなりません。
ここでバイトニック結合(Merge)という分割の後の整列処理を行う必要があります。Stage=1、Pass=0(本書ではPassが0の時にバイトニック分割、それ以外はまバイトニック結合と定義)から、Stage=1、Pass=1のマージは以下の「表:Bitonic Merge(Stage=1,Pass=1)」(表14.3「表:Bitonic Merge(Stage=1,Pass=1)」)ようにします。
上記の表のマージでは(0,1,2,3)の上昇形態、(4,5,6,7)の下降形態に分けて整列を行います。
- 3 < 7(インデックス:0と1)
- 98 < 12(インデックス:2と3)、要素をスワップ
- 66 > 78(インデックス:4と5)、要素をスワップ
- 6 > 5(インデックス:6と7)
これにより一つのバイトニック配列に結合が行われました。
最後にステージ3を行うとバイトニック配列から、整列された配列に置き換えることができます。ステージ2の段階でバイトニック配列ができており、配列を再分割することはできなくなっているため、ステージ3ではマージのみを行います。
このようにバイトニック分割(スプリット)と結合(マージ)を繰り返すことによって、整列化した配列に並び替えるのがバイトニック整列のアルゴリズムの標準実装です。