バイトニックマージを行なうためには、バイトニック配列を先んじて構築する必要があります。バイトニック配列がないと、マージができないためです。

まずバイトニック配列に整列するための手順を見てみましょう。例えば要素数が「8」の場合は、２つのステージに分けます。

例えば、ステージ０の比較では、以下の不等式が成立するときに値のスワップ（入れ替え）を行います。

ステージ１の2つの間隔の比較は、以下の場合に要素をスワップします。

ステージの「2,1」との記述には、２つの間隔の比較後に、1つ間隔の比較をすることを示しています。（「Stage=1, Pass=0」と「Stage=1、Pass=1」の2つを合わせただけです。）

よく見て頂くと、この比較は、(1,2,3,4)を上昇形態のバイトニック配列にし、（5,6,7,8）を下降形態の配列とします。これにより、(1,2,3,4)対(5,6,7,8)のバイトニック配列を構築することができます。

抑えておきたい点としては、各ステージの段階でバイトニック配列が作られていくことです。

これで8つの要素を使ったバイトニック配列が作ることが可能となります。

さらに要素数を増やして「16」の場合を考えみましょう。その場合、一つステージを増やして３つのステージに分けます。

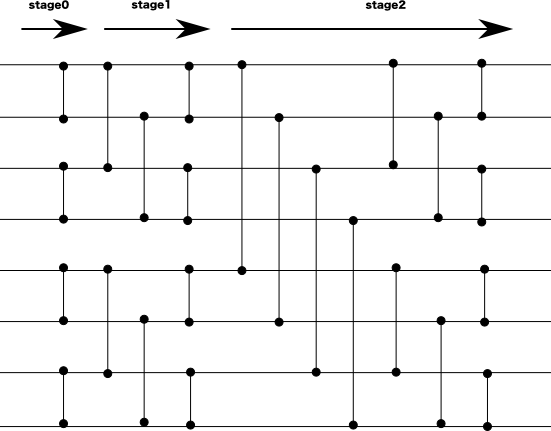
８つの要素数で使ったステージ０とステージ１を使い、新たなステージ２を追加すると、手順を以下のような図でまとめることができます。

図14.1 16個の要素のバイトニック整列（注意：図を縮小するため、8個の要素だけを表示）

このケースでは比較演算子が縦線に配置していると考えます。理解すべき点としては、各ステージの段階でバイトニック配列が作られていくことです。

この手順は、さらに要素数を増やし2の累乗と拡張ができます。例えば64個であれば、以下のように５つのステージに分けます。

これにより、32個の上昇していく配列と、32個の下降していくバイトニック配列ができます。各ステージの間隔が2の累乗で増加していることがわかるかと思います。