Warning
Reductionは一般的な数学や情報工学の用語です。この項目ではPrefix-Sumsの計算アルゴリズムの効率化をするための一手法とお考え下さい。時間を節約したい方はとばしていただいて構いません。
Reduction(還元)の基本的な考え方は数学的抽象性と一般性を持つため、解説の際には本来直感的に理解できるものを無駄に難しい数式を使って記述する傾向があるように思います。
無論、本書のターゲット読者は実務的にコードを設計する技術者のため、直感的なアプローチを取らせていただきます。
まずReductionについては筆者は一例を紹介しています。前の項目で解説した「表:Prefix-Sumの要素分解図」(Table 22.3, “表:Prefix-Sumの要素分解図(括弧内の数は式番号に該当)”)は、Reduction法に該当します。
Prefix-Sum(Table 22.2, “表:Prefix Sumの一例”)は配列の和を求めて上昇配列を構成しますが、Reduction法は配列の和を分解して、計算アルゴリズムのデータ並列化をします。
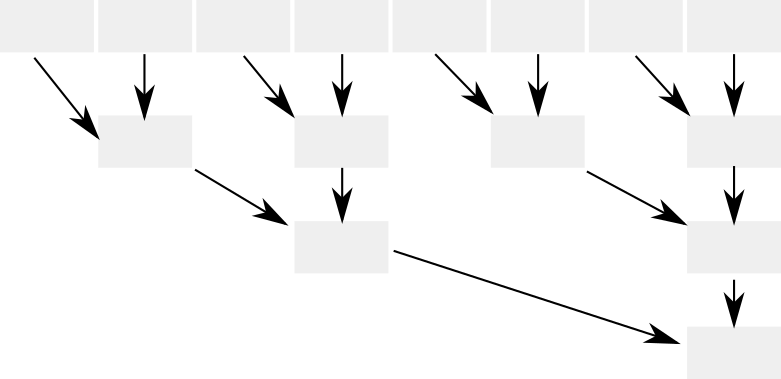
前の項目で解説したシーケンシャルなPrefix-Sumのアルゴリズムは、「図:シーケンシャルな還元」(Figure 22.2, “図:シーケンシャルな還元”)のように配列の左要素から部分和(掃き上げ)をしていきます。
シーケンシャルな還元は再帰(Recursion)として実装ができますが、パフォーマンスはデータサイズが増えるほど急激に劣化します。
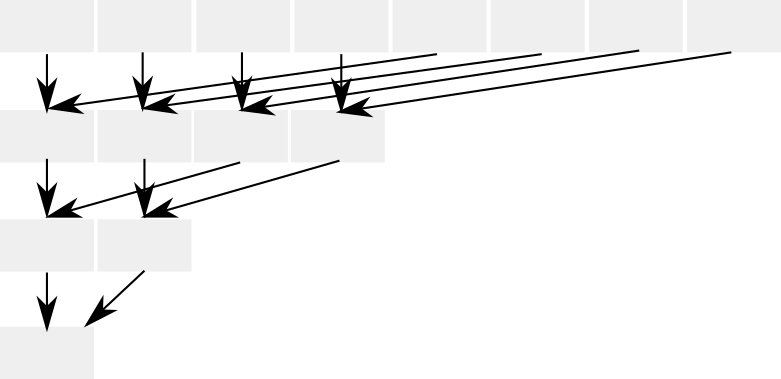
次にGPGPUを使った還元アルゴリズムの例ですが、「表:Prefix-Sumの要素分解図」(Table 22.3, “表:Prefix-Sumの要素分解図(括弧内の数は式番号に該当)”)を一般化すると、「図:並列化した還元」(Figure 22.3, “図:並列化した還元”)というような図式で表すことができます。
この方式はデータ並列化のための処方箋として加算演算の「結合性」(associativity)を利用しています。
結合性とは(1,2,3)の総和を計算する際にシーケンシャルな計算では(1+2)+3とするのに対して、1+(2+3)といったように部分和の再グループ化を可能とします。
つまり部分和を分解・再グループ化します。グループ化によって並列化できる要素を増やすことができます。ステップが進むと逆三角形、逆ピラミッドのようになるため、並列性は落ちますが、リソースをもっとも使うベースの部分和については、並列コアが飽和している状況が想定されるため、アルゴリズムの終結部のステップにいたるまでは、高い並列性を保つことができます。
この並列化を行うとSIMD使用率は「図:並列化した還元のSIMD使用パターン」(Figure 22.4, “図:並列化した還元のSIMD使用パターン”)のようになります。使用するレジスタが分散しており最適化の余地があります。つまり飛び地ができることで、SIMDのレジスタの未使用部分が増加し、大量のスレッドで並列コアを飽和させても、物理的リソースの多くが使用されない状況となります。
SIMDの使用率を改善するためのアルゴリズムも存在し、広く活用されています。飛び地を作らないためには、加算演算の「交換性」(commutativity)を利用して、加算する要素の添字をリファクタリングします。
交換性とは、(1,2,3,4)の総和を計算するときに、(1+4)+(2+3)=(5+5)=10といったように計算する順序を都合の良いように変えても、結果に影響を与えません。
この方式を使うと、並列コアのレジスタの飛び地を減らし、SIMDの使用率を大幅に上げることができます。