アクセスパターンを一言で表すなら、データ配列の要素を連続的でなく、ストライドのような飛び地を踏んでアクセスしないようするデータのパターンです。

1次元配列データのみの場合、アクセスパターンはあまり大きな問題ではなく、実際に1次元の配列を連続的にアクセスするようにするのは、あまり面倒なことではありません。１次元のアクセスパターンは、とにかくストライドやバンクコンフリクトを避けることに集中します。

2次元配列データでアクセスパターンはバッファオブジェクトは２次元配列をベクトル型を除きカーネルに渡せないので、1次元データ配列として擬似的に2次元配列を再現します。

以下のコードはホストメモリ側でカーネルに渡す行列データの一例です。

2次元配列. 

int[] A = new int[] {
    1,2,3,4,
    5,6,7,8,
    9,10,11,12,
    13,14,15,16
};

ここで見て頂きたい点としてはカラムという次元を1次元配列として表現していることです。例えば、行列対行列の乗算は行x列というかけ算をしますが、行は連続した添字でアクセスができますが、特定の列をアクセスする場合は、1,5,9というように連続的にアクセスができなくなります。

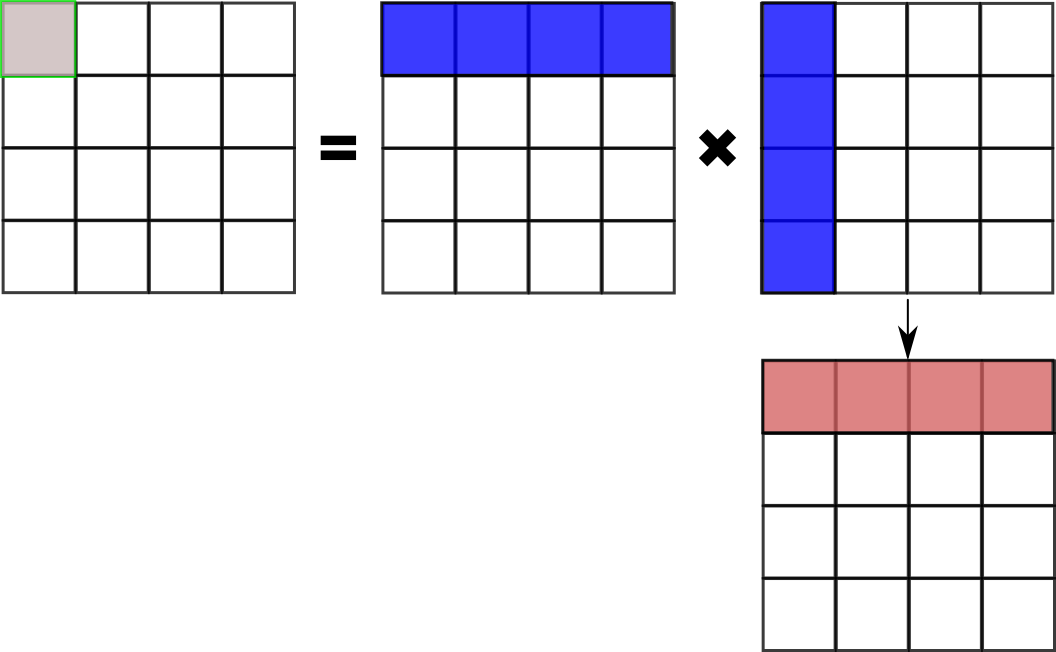
以下の図は行列乗算を2次元で表したものです。

図2.19 図：行列乗算のアクセスパターン（下部は転置後のパターン）

左辺は乗算の解です。解の一番左上のグレー色になっている（0,0）の座標の値を求めるには、右辺の左側行列の一行目と、右辺右側の行列の一列目を掛けます。

右下の行列は、連続的に配列要素にアクセスするために転置（transposition）しています。これにより右辺右側の行列も「１行目」に連続的にアクセスしながら乗算の計算ができるようになります。